728x90
문제:https://www.acmicpc.net/problem/11444
난이도: 골드 2
단순히 피보나치 수를 구하는 문제. 다만 n이 무지막지하게 큰.
아이디어 1
처음에는 분할 정복을 어떻게 쓸지 생각이 안 떠올랐다. 그렇게 고민을 하다가 피보나치 수를 직접 나눠서 써보기로 하였다.
우선 n이 짝수일 때이다. n=2k일 때 k번째 항까지 분할을 하였다.
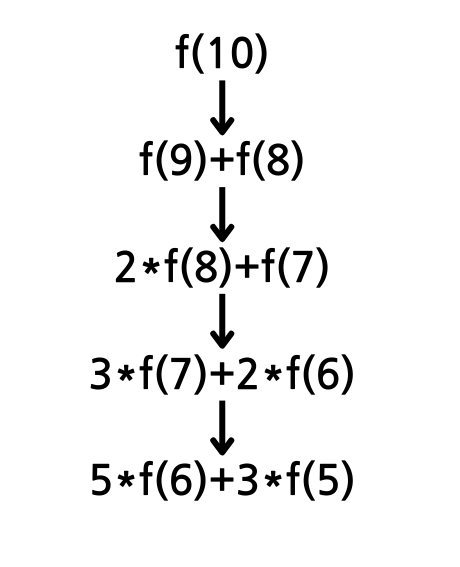
f(10)을 예시로 들어봤다. 2개로 계속해서 나누었을 때 항의 개수가 피보나치수열을 이루는 것을 알 수 있다. n/2까지 과정을 반복해 보면 다음과 같은 식을 얻을 수 있다.

다음은 n이 홀수 일 때다.

n=k//2+1이라 할 때 k번째 항까지 분할하였다. 일반항으로 나타내면 다음과 같다.

나도 왜 이런 식이 나오는지는 모른다. 2시간 정도 노트에다가 끄적여보며 알아낸 것이기 때문에 이유는 잘 모르겠다...
어쨌든 이런 규칙성을 얻었으니 재귀함수를 이용해 분할 정복을 구현해 주면 된다.
시도 1
import sys
input = sys.stdin.readline
n=int(input())
r=1000000007
t=[0,1,1,2,3]
def divide(x):
k=x//2
#print(x)
if x<=4:return t[x]
if(x%2==0):return (divide(k)%r) * ((divide(k+1)%r)+(divide(k-1)%r))%r
elif(x%2==1):return ((divide(k+1)%r)**2 + (divide(k)%r)**2)%r
print(divide(n))실패한 이유
결과는 시간초과. 이유는 한번 방문한 값을 계속해서 다시 연산함으로써 같은 연산이 반복해서 여러 번 일어났기 때문이다. 따라서 리스트를 만들어 연산을 할 때마다 값을 저장해 주면 시간을 줄일 수 있다.
정답 코드
import sys
input = sys.stdin.readline
n=int(input())
l1=[]
r=1000000007
p=[0,1,2,3,4]
q=[0,1,1,2,3]
def divide(x):
k=x//2
#print(x)
if x in p:return q[p.index(x)]
if(x%2==0):a=(divide(k)) * ((divide(k+1))+(divide(k-1)))%r
elif(x%2==1):a=((divide(k+1))**2 + (divide(k))**2)%r
p.append(x)
q.append(a)
return a
print(divide(n))
참고로 이 코드를 이용하여 나머지만 잘 조절해 주면 https://www.acmicpc.net/workbook/view/6512 여기 있는 문제들을 다 풀 수 있다. 레이팅 날먹
728x90
'문제풀이 > ETC' 카테고리의 다른 글
| 32224:물탱크 알바(easy) [백준 문제풀이][Python] (5) | 2024.09.07 |
|---|---|
| 17298:오큰수 [백준 문제풀이][Python] (6) | 2024.07.24 |
| 1202:보석 도둑 [백준 문제풀이][Python] (0) | 2024.07.15 |
| 1074 : Z [백준 문제풀이][C++] (0) | 2023.08.11 |
