문제:https://www.acmicpc.net/problem/1074
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net
문제에서도 설명하고 있듯이 재귀함수를 이용해 푸는 문제임을 알 수 있다.

배열에서 반복적으로 나오고 있는 Z를 살펴보면, 자신의 구역을 전부 돌고 다음 구역으로 이동하는 걸 볼 수 있다.
따라서 Z를 4분면처럼 4개로 나눠 생각한 뒤, (r,c)가 어디 속해 있는지를 크기가 다른 모든 Z에 대해 계산해주면 된다.
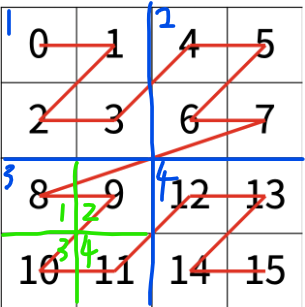
예제 입력 1의 출력 결과인 11을 가지고 예시를 들자면
파란색 Z에 대해서는 11은 3번째 칸에 속해있고
초록색 Z에 대해서는 11은 4번째 칸에 속해있다.
즉 11 = 4*(3-1) + 1*(4-1) 로 표현 할 수 있다.
이제 모든 n에 대해서 어느 사분면에 속해있는지 판별하는 식을 생각해보자.
우리가 수학에서 사분면을 따질때 기준은 x,y가 0보다 크냐, 작냐를 기준으로 따졌다.
그럼 여기서는 n으로 나눴을때 나머지를 기준으로 생각해주면 되지 않을까?
n=2인 배열에서 6(1,2)을 예시로 들어보자.
파란색 Z는 한변의 전체 길이가 2^2=4이므로 4로 나눠주게 되면
r%4=1,c%4=2
1은 n/2보다 작고 2는 n/2보다 크거나 같기 때문에 2번 구역에 들어간다는걸 알수있다.
위에서 어라 했던 분들도 있겠지만, 주의해야 될 점은 배열이기 때문에 index가 0부터 시작한다는 점과
행,열로 따지기 때문에 x,y를 뒤집어 생각해야되고, 수학의 사분면처럼 2,1,4,3이 아닌 1,2,3,4로 순서를 붙여야 되고,
마지막으로 행은 위에서부터 세기 때문에 구역을 결정할때 잘 결정해줘야 한다.
위에 이러한 점을 토대로 함수를 만들어주었다.
const int N=18;
ll n,r,c;
ll s[N];//각 크기에 따른 Z의 구역 값을 저장해주는 리스트
void chk(int n,int k){
ll y,x;//행,열
x = r%n;//나눈 값
y = c%n;//나눈 값
//어느 구역인지 판별
if(y>=(n/2) && x>=(n/2)) s[k]=4;
else if(y>=(n/2) && x<(n/2)) s[k]=2;
else if(y<(n/2) && x>=(n/2)) s[k]=3;
else if(y<(n/2) && x<(n/2)) s[k]=1;
}
이를 토대로 짠 전체 코드다.
#include<bits/stdc++.h>
#define rep(i,a,b) for (int i =a; i<=b; ++i)
using namespace std;
using ll = long long;
const int N=18;
ll n,r,c;
ll s[N];//각 크기에 따른 Z의 구역 값을 저장해주는 리스트
void chk(int n,int k){
ll y,x;//행,열
x = r%n;//나눈 값
y = c%n;//나눈 값
//어느 구역인지 판별
if(y>=(n/2) && x>=(n/2)) s[k]=4;
else if(y>=(n/2) && x<(n/2)) s[k]=2;
else if(y<(n/2) && x>=(n/2)) s[k]=3;
else if(y<(n/2) && x<(n/2)) s[k]=1;
}
int main(){
cin.tie(0)->sync_with_stdio(0);
cin >> n>>r>>c;
rep(i,1,n){//n번 반복
//2^i를 길이로 가지는 z에서의 구역을 리스트에 i번째에 넣어준다.
chk(pow(2,i),i);
}
ll res=0;
rep(i,1,n){
//s의 i번째 값을 가져와 곱해서 더해준다.(위에 있는 식 참고)
res+=(s[i]-1)*pow(4,i-1);
}
cout << res;
}

'문제풀이 > ETC' 카테고리의 다른 글
| 32224:물탱크 알바(easy) [백준 문제풀이][Python] (5) | 2024.09.07 |
|---|---|
| 17298:오큰수 [백준 문제풀이][Python] (6) | 2024.07.24 |
| 1202:보석 도둑 [백준 문제풀이][Python] (0) | 2024.07.15 |
| 11444:피보나치 6 [백준 문제풀이][Python] (0) | 2024.07.10 |
